数据结构与算法 --3. 图
一、图的定义
图 $G$ 由顶点集 $V$ 和边集 $E$ 组成,记为 $G=(V,E)$
$V={v_1,v_2,…,v_n}, \quad |V|$ 表示图中顶点的个数,也称为图 G 的阶
$E=\lbrace (u,v)|u \in V,v \in V \rbrace$
注释:图不能为空集
二、图的分类和术语
1. 有向图 / 无向图
2. 简单图 / 多重图
简单图:(1) 不存在重复边 (2) 不存在 $(u,u)$ 点
3. 完全图 (有向完全图 / 无向完全图)
任意两个点 $(u,v)$ 之间存在边 $(u,v)$
4. 子图
对于图 $G=(V,E)$ 和图 $G’=(V’,E’)$,如果 $V’ \in V$,$E’ \in E$,则 $G’$ 是 $G$ 的一个子图,默认图的自身也是子图
5. 连通,连通图,连通分量(无向图中考虑)
连通:当且仅当 $u,v$ 存在一条路径,称为 $u,v$ 连通
连通图:图中任意两点皆连通
连通分量:极大连通子图
6. 强连通,强连通图,强连通分量(有向图中讨论)
7. 生成树,生成森林
只有连通图可以考虑生成树,非连通图只能考虑生成森林
生成树:极小连通子图 $V’=V$(极小指的是边最少)
生成森林:非连通图的每个连通分量都有一个生成树
8. 顶点的度(无向图或无向图),入度 / 出度(有向图)
$d_i:v_i$ 的边数
$\sum d_i = 2e$
$\sum id_i = e$
$\sum od_i = e$
9. 边的权值,网 (带权图)
10. 稠密图,稀疏图(没有严格的定义)
$|E| < |V|log|V|$
11. 路径,路径长度,回路 / 环 / 圈
路径长度:$u$ 到 $v$ 经过的边数
$e < n-1$:非连通
$e > n-1$:一定有环
12. 简单路径,简单回路
简单路径:顶点不重复
简单回路:除首末节点,不存在重复顶点
13. 距离
若 $u,v$ 存在路径,最短的路径长度称为距离
14. 有向树
${\exists} v_o, \;\; id_{v_o}=0$
其余 $v_i \;\; id_{v_o}=1$
三、图的存储和基本操作
1. 邻接矩阵法:有 $n$ 个顶点,用一个 $n \times n$ 的矩阵存储
$a [i,j]$ 用来表示顶点 $i$ 到顶点 $j$ 是否有边
有向权值图的权值可能是 0 也可能是负数,所以用 $\infty$ 表示 $u,v$ 之间不存在边
$A^n [i][j]$:表示顶点 $i$ 到顶点 $j$ 当中路径长度 $=n$ 的路径条数(后面会证明)
2. 邻接表
优点:方便找到与顶点相邻的边
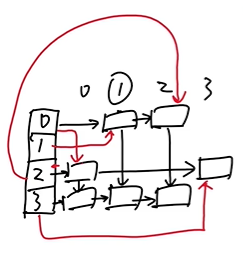
3. 十字链表
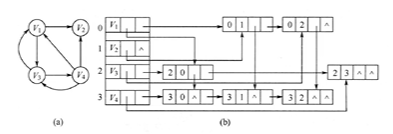
Q:怎么画十字链表?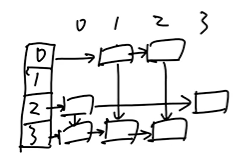
4. 邻接多重表
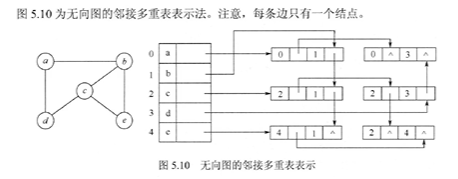
四、图的遍历
1. 广度优先搜索 BFS
操作
标记起始节点,并把起始节点入队
从队列中弹出一个元素,访问,并把该元素的未标记的相邻节点入队
复杂度
时间复杂度:$\begin {cases}
O (n^2), & \text {邻接矩阵} \\
O (n+e), & \text {邻接表}
\end {cases}$
空间复杂度:$O (n)$
无权值图的最短路径
广度优先生成树
2. 深度优先搜索 DFS
操作
访问相邻的未标记节点
如果没有相邻的未标记节点,则向上回溯
复杂度
时间复杂度:$\begin {cases}
O (n^2), & \text {邻接矩阵} \\
O (n+e), & \text {邻接表}
\end {cases}$
空间复杂度:$O (n)$
连通性、连通片数量
如果回溯到了起始节点,但是还有未标记的节点,代表图是非连通的
则在未标记的节点中随机选择一个节点,并重复遍历动作
可以根据 DFS 被调用的次数,判断连通片的数量
深度优先生成树
五、最小生成树
1. 概念
生成树:连通图中的最小连通子图(边最少)
最小生成树:带权图中权值和最小的生成树
不同的最小生成树,权值合都是相同的
2. 算法
(1) Prim 算法:保持连通,选最小边及其顶点(最小边 = 最权值小的边)
从某一个顶点开始,不断加顶点和边
思路:贪心算法(每一步都考虑当前最优,结果恰好是全局最优,前提是满足最优子结构)
时间复杂度:$O (n^2)$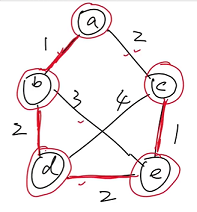
(2) Krushal 算法:保持无圈,选最小边
先包含全部的节点,因为生成树的节点数都是一样的
思路:贪心算法
时间复杂度:$O (eloge)$
(3) 破圈法:找一个圈,删除最大边
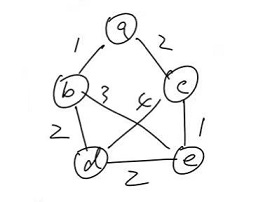
圈:$abdeca$,删除 $de$ 边 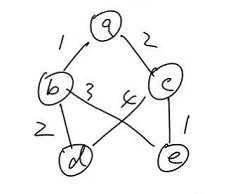
圈:$abdca$,删除 $dc$ 边 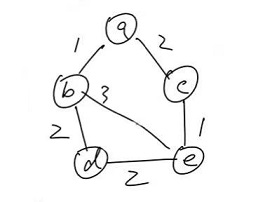
圈:$abeca$,删除 $be$ 边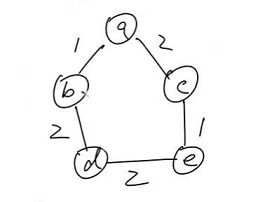
六、最短路径
1.Dijkstra 算法:求单源最短距离(权值非负的有向图)
思想:贪心算法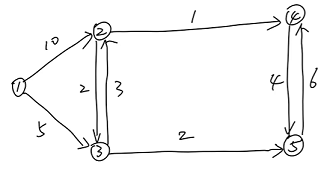
(1) 将每个点标记一个距离值
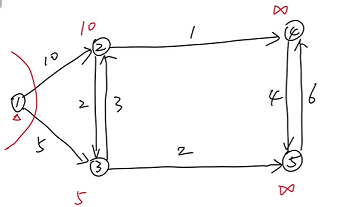
(2) 选取最小的顶点,加进来
(3) 修改该点的出边的距离值
若通过该点到达的距离比较近,则修改距离值,并标记前驱节点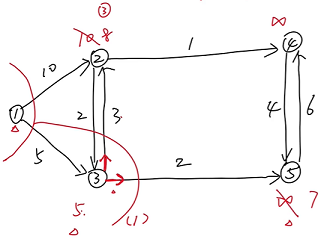
(4) 重复该过程,直到全部的点被加进来
时间复杂度:$O (n)$
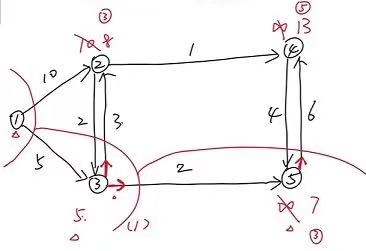
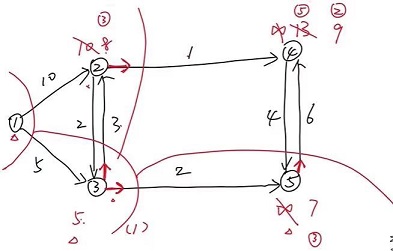
例:节点 1 到节点 4 的最短路径?
找节点 4 的前驱标记,是 3;再找节点 3 的前驱标记,依次重复
1->3->2->4
2.Floyd 算法:求各顶点值间最短路径(可以有负权值,但不可以有含负权值的环)
思想:动态规划
$A^{(k)}_{i,j}$:$i$->$j$ 在顶点集 $\lbrace 1,2,…,k \rbrace$ 中的最短路径
路径集合 $S^{(k)}$ 有两种:
(1) 包含 k 的:$A^{(k-1)}_{i,k}+A^{(k-1)}_{k,j}$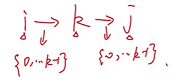
(2) 不包含 k 的:$A^{(k-1)}_{i,j}$
于是可以推得公式:$A^{(k)}_{i,j}=min \lbrace A^{(k-1)}_{i,j},A^{(k-1)}_{i,k}+A^{(k-1)}_{k,j} \rbrace$
七、拓扑排序
应用场景:有向无环图 (AOV 网),顶点代表的是事件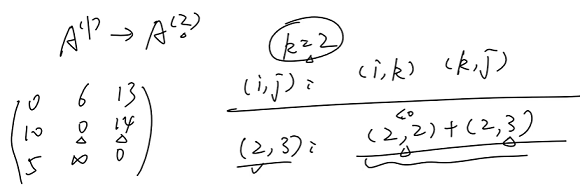
$i$->$j$:$i$ 必须完成,才能开始 $j$
(1) 选择一个入度 = 0 的点
(2) 删除该点的所有出边
(3) 重复这两个步骤,直到
$\begin {cases}
没有点了:得到一个合法的拓扑排序 & \text {} \\
有点但是没有入度为 0 的点:图中有环 & \text {}
\end {cases}$
八、关键路径
1. 概念
应用场景:有向带权图,顶点代表事件,边代表活动,权值代表开销 (时间)->AOE 网
顶点不是重点,顶点只是表示入边代表的事件已经完成了
关键路径:在 AOE 网中寻找最长路径(最短工期:完成 $e_1-e_5$ 最少需要的时间)
关键路径是不唯一的
目的:缩短关键路径,缩短工期
关键活动:关键路径上的边所代表的活动
2. 算法概念
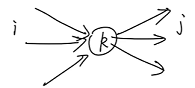
(1) $ve (k)$:顶点 k 的最早时间
$ve ($ 源点 $)=0$
$ve (k)=max \lbrace ve (i)+w (i,k) \rbrace$
(2) $vl (k)$:顶点 k 最迟时间
(3) $ve (k)=vl (k)$:工期不变
$vl (k$$)=min \lbrace vl (j)-w (k,j) \rbrace$
(4) $e ()$:边的最早时间
$e (e_ik)=ve (i)$
(5) $l ()$:边的最迟时间
$l (e_kj)=l (j)-w (k,j)$
(6) $d ()=l ()-e ()$
$d ()=0$ 是关键活动
3. 例子
4. 缩短工期:缩短所有关键路径
(1) 公共边
(2) 每个路径选一个
5. 总结
$ve ()$:起点加权取最大
$vl ()$:终点减权取最小
$e ()$:就取起点最早值
$l ()$:终点最迟减权值
数据结构与算法系列
数据结构与算法 —1. 线性表
数据结构与算法 —2. 树
数据结构与算法 —3. 图
数据结构与算法 —4. 查找
数据结构与算法 —5. 排序