数据结构与算法 --4. 查找

發表於 2019-03-31 更新於 2021-07-01 分類於大学课程-数据结构与算法

一、概念

1. 查找：在数据集合 (查找表) 中寻找满足某种条件的数据元素的过程。

查找表：$\begin {cases}
静态查找表： & \text {} \\
动态查找表：有增删 & \text {}
\end {cases}$
查找的结果一般分为两种：
(1) 查找成功：在数据集合中找到了满足条件的数据元素
(2) 查找失败

2. 关键字

3. 平均查找长度 $ASL = \sum_{i=0}^n P_iC_i$

二、顺序查找、折半查找、分块查找

1. 顺序查找：依次查找表中元素

(1) 一般线性表 (无序) 中的查找

for (int i=0, i<n, i++)
{
	// 对 a [i] 判断
}

$ASL_{成功} = \displaystyle {1 \over n}(1+2+…+n)={n+1 \over 2}$
$ASL_{失败} = n$

(2) 有序表的顺序查找：失败时，可提前返回

$ASL_{成功} = \displaystyle {n+1 \over 2}$
$ASL_{失败} = \displaystyle {1 \over n+1}(1+2+…+n+n) = {n \over 2} + {n \over n+1}$
$n$ 个分支节点是树有 $n+1$ 个叶子

2. 折半查找：有序的顺序表中

int Binary_Search (SeqList L, ElemType key)
{
	int low=0, high=L.TableLen-1, mid;
	while (low < high)
	{
	    mid = (low + high) / 2;
	    if (L.elem [mid] == key)
	        return mid;
	    else if (L.elem [mid] > key)
	        high = mid - 1;
	    else
	    	low = mid + 1;
	}

	return -1;
}

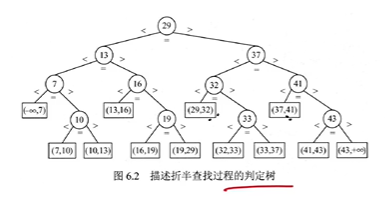
判定树是一个平衡二叉树
判定树的高度：$\lceil log_2 (n+1) \rceil$ 或 $\lfloor log_2 (n) \rfloor + 1$
$ASL_{成功} = \displaystyle {1 \over 11}(1 \times 1 + 2 \times 2 + 3 \times 4 + 4 \times 4) = 3$
$ASL_{失败} = \displaystyle {1 \over 12}(3 \times 4 + 4 \times 8) = {11 \over 3}$
可以构成折半查找的序列：某数字后面的数字都与其有相同的大小关系

3. 分块查找：块间有序，块内无序

快的索引表是有序的，所以也可以顺序查找或是二分查找
问题：怎么分块，效率最高？
假设有 $n$ 个元素，$s$ 个元素一个块，块数总共有 $\displaystyle \lceil {n \over s} \rceil$
$ASL_{成功} = \displaystyle \frac {\frac {n}{s}+1}{2} + {s+1 \over 2}$

$\quad \quad \quad \; \displaystyle ={s \over 2} + {n \over 2s} + 1$

$\quad \quad \quad \; \geq \displaystyle 2 \sqrt {\frac {s}{2} \times \frac {n}{2s}} + 1 $

$\quad \quad \quad \; = \sqrt {n} + 1 $

等号成立的条件：$\displaystyle {s \over 2} = {n \over 2s} $ => $s=\sqrt {n}$

三、B 树（多路平衡查找树）

1.B 树及其基本操作

B 树中所有节点的孩子节点数的最大值称为 B 树的阶，通常用 $m$ 表示

(1) 树中每个节点至多有 $m$ 棵子树

(2) 若根节点不是终端节点，则至少有两棵子树

(3) 除根节点外的所有非叶节点至少有 $\displaystyle \lceil {m \over 2} \rceil$ 个

(4) 非叶节点的结构如下

$n$：关键字的个数（$\displaystyle \lceil {m \over 2} \rceil -1 \leq n \leq m-1$）

(5) 关键字 $+1=$ 子树数

$\displaystyle \lceil {m \over 2} \rceil \leq $ 子树数 $ \leq m$
根是特殊情形：$2 \leq $ 子树数 $ \leq m$

(6) 关键字数 $m$ 与高度 $h$ 的关系

每个节点最多有 $m$ 个子树，第 $m$ 层最多总共有 $m^i$ 个子树，总共有 $(m-1) m^i$ 个关键字

$1+2 (\lceil {m \over 2} \rceil -1)(1+ \lceil {m \over 2} \rceil + …+{\lceil {m \over 2} \rceil}^{h-2}) \leq n \leq (m-1)[1+m+m^2+…+m^{h-1}]$

$1+2 \times (\lceil \frac {m}{2} \rceil -1) \times \displaystyle \frac {{\lceil \frac {m}{2} \rceil}^{h-1} - 1}{\lceil \frac {m}{2} \rceil -1} \leq n \leq (m-1) \times {m^h-1 \over m-1}$

$2 {\lceil \frac {m}{2} \rceil}^{h-1} - 1 \leq n \leq m^h - 1$

$log_m (n+1) \leq h \leq log_{\lceil \frac {m}{2} \rceil} \displaystyle ({n+1 \over 2}) +1$

2. 查找

节点上查找 $\begin {cases}
成功 & \text {} \\
失败：子树查找 & \text {}
\end {cases}$

3.B 树插入

(1) 定位：某个非叶节点

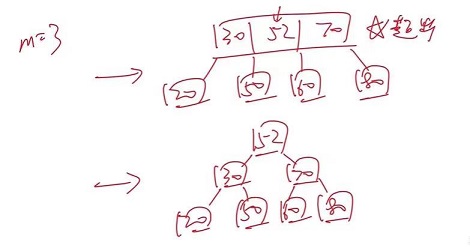
(2) 插入：若插入之后，关键字数目 $=m$，分裂，将 $\displaystyle \lceil \frac {m}{2} \rceil$ 关键字插入父节点

4.B 树删除

分层两大类情形：

(1) 删除的节点是最底层分支

$\quad$(a) 欲删除节点的父节点关键字 $> \lceil \frac {m}{2} \rceil -1$，直接删除
$\quad$(b) 欲删除节点的父节点关键字 $= \lceil \frac {m}{2} \rceil -1$
$\quad \quad$ (i) 兄弟节点够借：关键字 $\leq \lceil \frac {m}{2} \rceil -1$
$\quad \quad \quad$ 父子易位，再平衡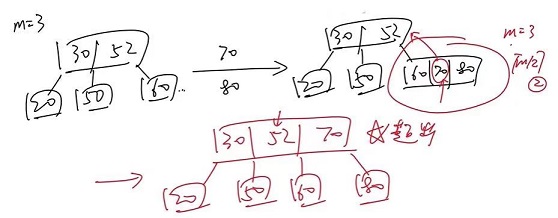

$\quad \quad$ (ii) 兄弟节点不够借：关键字 $= \lceil \frac {m}{2} \rceil -1$
$\quad \quad \quad$ 合并 (左 / 右 + 父亲 + 自己)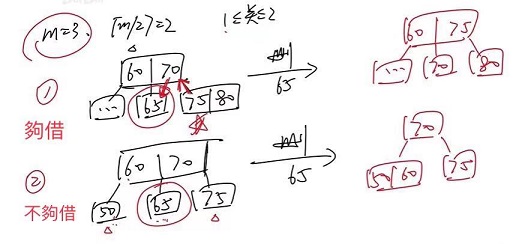

Q：为什么能合并，不会超过关键字数量的上界吗？
合并：$(\lceil \frac {m}{2} \rceil -1) + 1 + (\lceil \frac {m}{2} \rceil -2)=$