通信原理 --(2)信道
通信原理 —(1)绪论
通信原理 —(2)信道
通信原理 —(3)模拟调制技术
通信原理 —(4)模拟信号数字化
通信原理 —(5)数字基带传输
通信原理 —(6)数字频带传输
通信原理 —(7)最佳接收
通信原理 —(8)同步
一、信道的概念和实际信道
1. 信道的概念
为什么要研究信道?因为信道会导致信号的变化
如何研究信道?建立数学模型 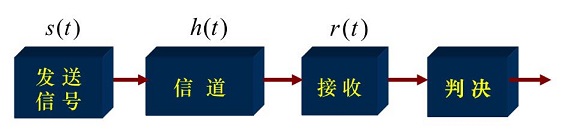
$r (t) = s (t) \oplus h (t) + n (t)$
从信号处理角度看,信道就是一个滤波器,$h (t)$ 是滤波器的冲激响应。
从信号与系统的角度看,信道就是一个系统,$h (t)$ 是系统的冲激响应。
对于信道来说,$h (t)$ 就是信道的冲激响应,也称信道的特性。
2. 实际无线信道
(1) 电磁波频谱划分
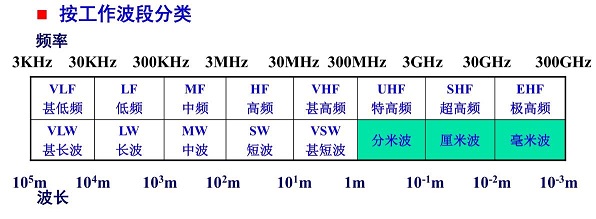
(2) 电磁波的特性
电磁波频率越高,通信波束越窄 (功率利用越充分),天线发射效率越高 (天线口径可越小),
穿透能力越强,绕射能力越弱
(3) 电磁波主要传播方式
(a) 天波传播:短波 (3M-30MHz)、电离层的反射 (频率低易反射)
(b) 地波传播:长波、绕射
(c) 散射传播:微波、对流程的散射、大容量战略通信
(d) 视距传播:超短波、微波(地面的远距传播必须设置中继站)
3. 实际有线信道
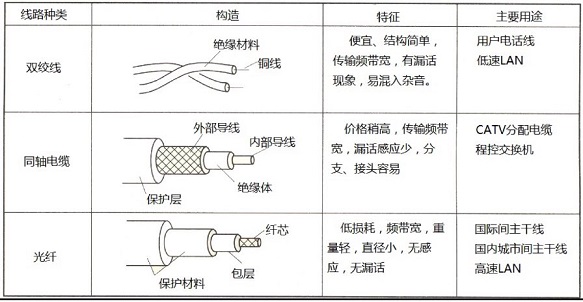
(1) 双绞线
Q:为什么要进行扭绞?
A:为了提高抗干扰性能,绞度越大,抗干扰能力越好,同时成本也越高
Q:为什么纽绞可以提高抗干扰特性?
A:从理论上讲,电路形成的环路围绕的面积越大,就月容易被干扰信号影响。双绞线将环路面积减到最小,所以抗干扰能力强。两根非常接近的铜线都在传导电信号时,就会出现一定的电磁干扰,这种干扰称作串扰。如果把电极相反的一根铜线相互绞在一起,可以减少串扰以及信号放射程度,每一根缠绕着的导线在导电时,发出的电磁幅射被绞合的另一根线上发出的电磁辐射所抵消,随着单位长度电缆中所缠绕的线的对数的增加,防止串饶的能力也增加。
(2) 同轴电缆
(3) 光纤
光纤的色散限制了光纤的无中继传输距离
延申阅读:如何利用光子的轨道角动量 (OAM) 进一步提高光通信的传输速率和频带利用率?关于 OAM 的光通信要解决的关键问题有哪些?如何解决?
二、信道的数字模型和信道特性
1. 信道特性及其数学模型
(1) 调制信道和编码信道
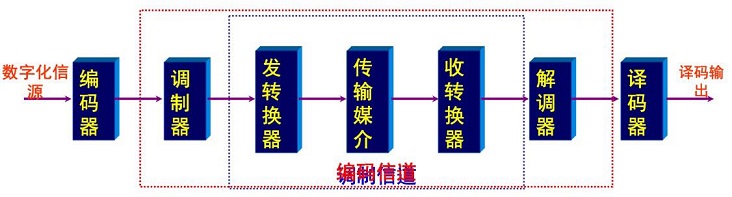
(2) 二对端的调制信道模型
$e_o (t) = k (t) \cdot e_i (t) + n (t)$
加性干扰 $n (t)$:即使没有信号输入,接收端仍有信号输出
乘性干扰 $k (t)$:恒参信道、随参信道
(a) 加性噪声恒参信道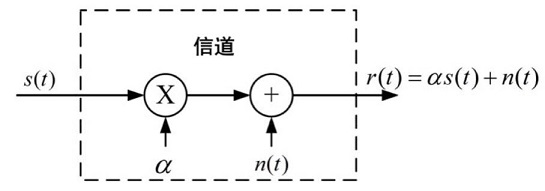
(b) 具有加性噪声的线性滤波信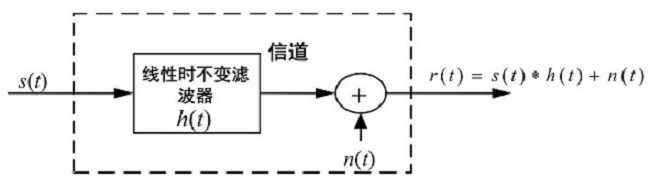
(c) 具有加性噪声的时变线性滤波信道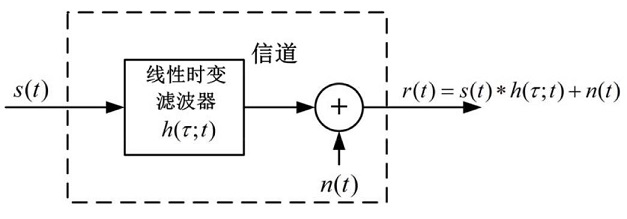
(3) 编码信道模型:采用数字信号的转移概率来描述
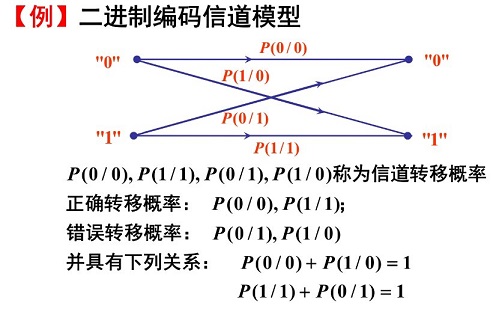
2. 信道特性对信号传输的影响
信道的传输特性可以用其幅频特性和相频特性来描述 (适用于恒参信道)。
信道引起的失真:
(1) 码间串扰
(a) 传输特性不理想,导致前后码元波形畸变并使前面波形出现拖尾,从而对当前码元的判决造成干扰。
(b) 多径延迟使得基带码元重叠,也会造成码间串扰。
(2) 频率偏移:多普勒效应
(3) 信号衰落
移动通信中信号随接受机与发射机之间的距离不断变化即产生了衰落。其中,信号强度曲线的中直呈现慢速变化
,称为慢衰落;曲线的瞬时值呈快速变化,称快衰落。可见快衰落与慢衰落并不是两个独立的衰落(虽然他们的
产生原因不同),快衰落反映的是瞬时值,慢衰落反映的是瞬时值加权平均后的中值。
(a) 快衰落:主要原因是多径传输。
快衰一般服从瑞利(Rayleigh)分布、莱斯(Rice)分布或纳卡迦米(Nakagami)分布。
- 时间选择性衰落:主要原因是多普勒效应,交织编码可以克服时间选择性衰落。
- 频率选择性衰落:原因多是时延扩展
- 空间选择性衰落:在无线通信系统中天线的点波束产生了扩散而引起了空间选择性衰落。
(b) 慢衰落:主要原因是传输媒质结构发生变化。
对流层散射传播中,慢衰落通常服从对数正态分布。
# 时延扩展:
多径效应(同一信号的不同分量到达的时间不同)引起的接受信号脉冲宽度扩展的现象称为时延扩展。
时延扩展(多径信号最快和最慢的时间差)小于码元周期可以避免码间串扰,超过一个码元周期(WCDMA 中一个码片)需要用分集接收,均衡算法来接收。
# 相关带宽:
相关带宽内各频率分量的衰落时一致的也叫相关的,不会失真。
载波宽度大于相关带宽就会引起频率选择性衰了使接收信号失真。
3. 信道中的噪声和干扰
三、信道容量
1. 信道容量的概念
信道中信息能够无差错传输的最大平均信息速率。
2. 连续信道的信道容量
(1) 香浓公式
对于带宽有限、平均功率有限的高斯白噪声连续信道,设信道带宽为 $B (Hz)$,信道输出信号功率为 $S (W)$,输出加性高斯白噪声功率为 $N (W)$,则可以证明该信道的信道容量为 $\displaystyle C = B \log_2 (1 + {S \over N}) (b/s)$
令加性高斯白噪声的单边功率谱密度为 $n_0$,则 $N=n_0 B$
(2) 信道容量极限:即使带宽无穷大,信道容量也是有限值
$\displaystyle \lim \limits_{B \to \infty} C = \lim \limits_{B \to \infty} [{B n_0 \over S} \log_2 (1+ {S \over Bn_0})] \cdot {S \over n_0} = 1.44 {S \over n_0}$
使用到极限:$\displaystyle \lim \limits_{x \to 0} \log {1+x \over x} = 1$
证明:
$\displaystyle \lim \limits_{x \to 0} \log {1+x \over x}$
$= \displaystyle \lim \limits_{x \to 0} {1 \over x} \cdot \log (1+x) $
$= \displaystyle \lim \limits_{x \to 0} \log (1+x)^{1 \over x}$
$= \log e$
$= 1$
若底数为 $2$,利用换底公式:$\displaystyle \log_a N = {log_m N \over log_m a}$
(3) 带宽无穷大,保证无差错极限信息传输速率的最小信噪比为 $-1.6dB$
该值通常称为 $AWGN$ 信道的极限信噪比,或是香浓极限。
推导:
令信息传输速率 $R=C$,比特平均能量为 $E_b$,信道容量极限可以表示为:
$\displaystyle \lim \limits_{B \to \infty} = 1.44 {S \over n_0} = 1.44 {E_b C \over n_0}$
$=> \displaystyle {E_b \over n_0} = {1 \over 1.44} = -1.6dB$
3. 离散信道的信道容量
习题
- 恒参信道等效模型如图,试分析信号通过该信道传输时会产生哪些失真?
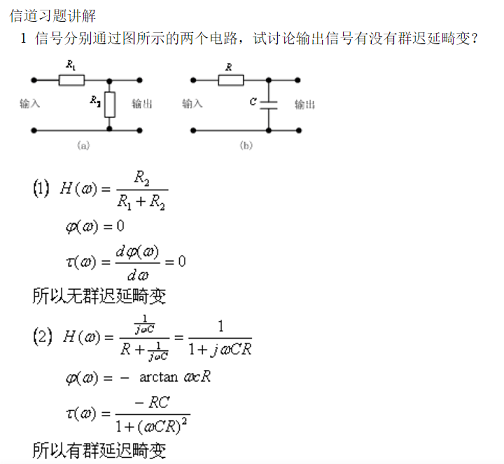
由《信号与系统》课程可知,
网络的传输特性 $H (w)$ 通常可用幅频特性 $|H (w)|$ 和相频特性 $\phi (w)$ 来表征 $H (w) = |H (w)| e^{\phi (w)}$。