机器学习算法 --（1）线性回归和非线性回归

發表於 2020-11-06 更新於 2021-11-08 分類於大学课程-机器学习

前言

1. 数据挖掘和机器学习的关系

2. 训练数据 vs 验证数据 vs 测试数据

3. 监督学习 vs 无监督学习 vs 半监督学习

4. 回归 vs 分类 vs 聚类

一、一元线性回归概念

回归：高尔顿提出
回归分析：建立方程模拟两个或多个变量之间如何关联
一个线性回归：包含一个自变量和一个应变量，用一条直线来模拟
一元线性回归的模型：$h_\theta (x) = \theta_0 + \theta_1x$
$\theta_0$ 是截距，$\theta_1$ 是斜率

二、代价函数

$\displaystyle J (\theta_0,\theta_1) = {1 \over 2m} \sum_{i=0}^m (h_\theta (x_i) - y_i)^2$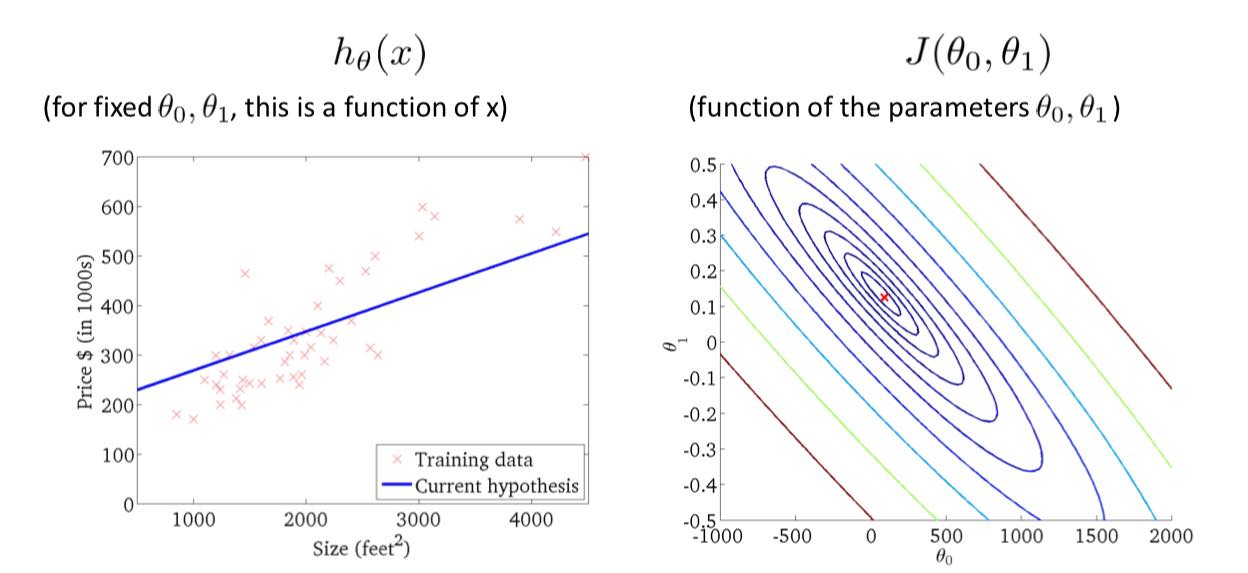

自变量是 $\theta_0$ 和 $\theta_1$，应变量是代价函数 $h_\theta (x)$，
本来是一个三维的函数图像，Z 轴是 $J (\theta_0,\theta_1)$，但是这里用等高线表示。
Q：如何寻找使得代价函数最小的 $\theta_0$ 和 $\theta_1$，后面会讲解。

三、相关系数和决定系数

决定系数

总平方和（SST）：$\sum_{i=0}^n (y_i - \bar y)^2$
残差平方和（SSE）：$\sum_{i=0}^n (y_i - \hat y)^2$
回归平方和（SSR）：$\sum_{i=0}^n (\hat y - \bar y)^2$
它们三者的关系是：$SST = SSE + SSR$
决定系数：$\displaystyle R^2 = {SSR \over SST} = 1 - {SSE \over SST}$

四、梯度下降法

概念

缺点：初始值的选取会影响到最后的结果，只能找到局部最优解
(凸函数的局部最值就是全局最值)
repeat until convergence
{
$\displaystyle \qquad\qquad\theta_j := \theta_j - \alpha {\partial \over \partial\theta_j} J (\theta_0,\theta_1)$ $\quad (for\quad j = 0 \quad and \quad j = 1)$
}

同步更新：
$\displaystyle temp0 := \theta_0 - \alpha {\partial \over \partial\theta_0} J (\theta_0,\theta_1)$
$\displaystyle temp1 := \theta_1 - \alpha {\partial \over \partial\theta_1} J (\theta_0,\theta_1)$
$\theta_0 := temp0$
$\theta_0 := temp1$

学习率 $\alpha$ 不能太大也不能太小，
太大可能会导致在收敛值附近不断震荡，一直无法收敛；
太小会导致收敛速度过慢

用梯度下降法来求解线性回归

$h_\theta (x) = \theta_0 + \theta_1x -(1)$
$\displaystyle J (\theta_0,\theta_1) = {1 \over 2m} \sum_{i=0}^m (h_\theta (x_i) - y_i)^2 -(2)$
$ 将 (1) 式代入 (2) 式 $
$\displaystyle {\partial \over \partial\theta_0} J (\theta_0,\theta_1) = {1 \over m}\sum_{i=0}^m (h_\theta (x_i) - y_i)$

五、sklearn 实现一元线性回归（sklearn 使用的是标准方程法）

x_data = data [:,0,np.newaxis]
y_data = data [:,1,np.newaxis]
# 创建并拟合模型
model = LinearRegression ()
model.fit (x_data, y_data)

# 画图
plt.plot (x_data, y_data, 'b.')
plt.plot (x_data, model.predict (x_data), 'r')
plt.show ()

六、多元线性回归

Hypothesis:

$h_\theta (x) = \theta^Tx = \theta_0x_1 + \theta_2x_2 + … + \theta_nx_n$

Parameters:

theta_0,theta_1,…,theta_n

Cost Function

$\displaystyle J (\theta_0,\theta_1,…,\theta_n) = {1 \over 2m} \sum_{i=0}^m (h_\theta (x_i) - y_i)^2 -(2)$

Gradient descent

repeat until convergence
{
$\displaystyle \qquad\qquad\theta_j := \theta_j - \alpha {\partial \over \partial\theta_j} J (\theta_0,…,\theta_n)$
$\displaystyle \quad\qquad (for\quad j = 0,1,…,n)$
}

七、多项式回归

原理

假设要拟合的不是直线（或超平面），而是需要找到一个用多项式所表示的曲线（或者超平面）。

sklearn 实现多项式回归

from sklearn.preprocessing import PolynomialFeatures
# 定义多项式回归，degree 的值可以调节多项式的特征
poly_reg = PolynomialFeatures (degree=1)
# 特征处理
x_poly =  poly_reg.fit_transform (x_data)
# 定义回归模型
lin_reg = LinearRegression ()
# 训练模型
lin_reg.fit (x_poly, y_data)

# 画图
plt.plot (x_data, y_data, 'b.')
plt.plot (x_data, lin_reg.predict (x_poly), c='r')
plt.show ()

八、标准方程法（vs 梯度下降法）

概念

$\displaystyle J (\theta_0,\theta_1,…,\theta_n) = {1 \over 2m} \sum_{i=0}^m (h_\theta (x_i) - y_i)^2 -(2)$
令 $\displaystyle {\partial \over \partial\theta_j} J (\theta)=…=0$
求解：$\theta_1,\theta_2,…,\theta_n$

例：X 为 $4 \times 5$ 矩阵，$4$ 个样本，$4+1$ 个参数

$X=
\begin {bmatrix}
1 & 2104 & 5 & 1 & 45 \\
1 & 1416 & 3 & 2 & 40 \\
1 & 1534 & 3 & 2 & 30 \\
1 & 852 & 2 & 1 & 36 \\
\end {bmatrix}
$ $\quad\quad$ $w=
\begin {bmatrix}
w_0 \\
w_1 \\
w_2 \\
w_3 \\
w_4 \\
\end {bmatrix}
$ $\quad\quad$ $y=
\begin {bmatrix}
460 \\
232 \\
315 \\
178 \\
\end {bmatrix}
$

$\sum_{i=0}^m (h_w (x_i) - y_i)^2=(y-Xw)^T (y-Xw)$

$\displaystyle {\partial (y-Xw)^T (y-Xw) \over \partial w} = 0$
$\displaystyle {\partial (y^Ty - y^TXw - w^TX^Ty + w^TX^TXw) \over \partial w} = 0$
$\displaystyle {\partial y^Ty \over \partial w} - {\partial y^TXw \over \partial w} - {\partial w^TX^Ty \over \partial w} + {\partial w^TX^TXw \over \partial w} = 0$
$0 - X^Ty - X^Ty + 2X^TXw = 0$
$X^TXw = X^Ty$
$w = (X^TX)^(-1) X^Ty$
注释：矩阵的求导

标准方程法 vs 梯度下降法

梯度下降法	标准方程法
缺点：需要选择合适的学习率需要迭代很多个周期只能得到最优解的近似值	优点：不需要学习率不需要迭代可以得到全局最优解
优点：当特征值非常多的时候也可以很好的工作	缺点：需要计算 $(𝑋^T𝑋)^{−1}$ 时间复杂度大约是 O ($n^3$) n 是特征数量

自己写标准方程法

def weights (xArr, yArr)
	xMat = np.mat (xArr)
	yMat = np.mat (yArr)
	xTx = xMat.T * xMat # 矩阵乘法
	# 如果矩阵的 det 值为零，说明该矩阵没有逆矩阵
	if np.linalg.det (xTx) == 0.0:
		print ("This matrix cannot do inverse")
		return
	#xTx.I 为 xTx 的逆矩阵
	ws = xTx.I * xMat.T * yMat
	return ws

九、特征缩放

假设不同的特征的取值范围相差非常大，就会造成天然的权重不一
解决方法：特征缩放

数据归一化

转化成 $(0,1)$ 之间：$newValue = \displaystyle {oldValue - min \over max - min}$

转化成 $(-1,1)$ 之间：$newValue = (\displaystyle {oldValue - min \over max - min}-0.5) \times 2$

数据标准化

$newValue = \displaystyle {oldValue - u \over s}$ 其中 u 为数据的平均值，s 为数据的方差

十、交叉验证法

若样本数据较少时，可以一部分作为训练集，一部分作为测试集，没有验证集。
例如有 100 组数据，可以 80 组作为训练集，20 组作为测试集。
但是当样本更少，8/2 拆分也不适合的时候，就可以使用交叉验证法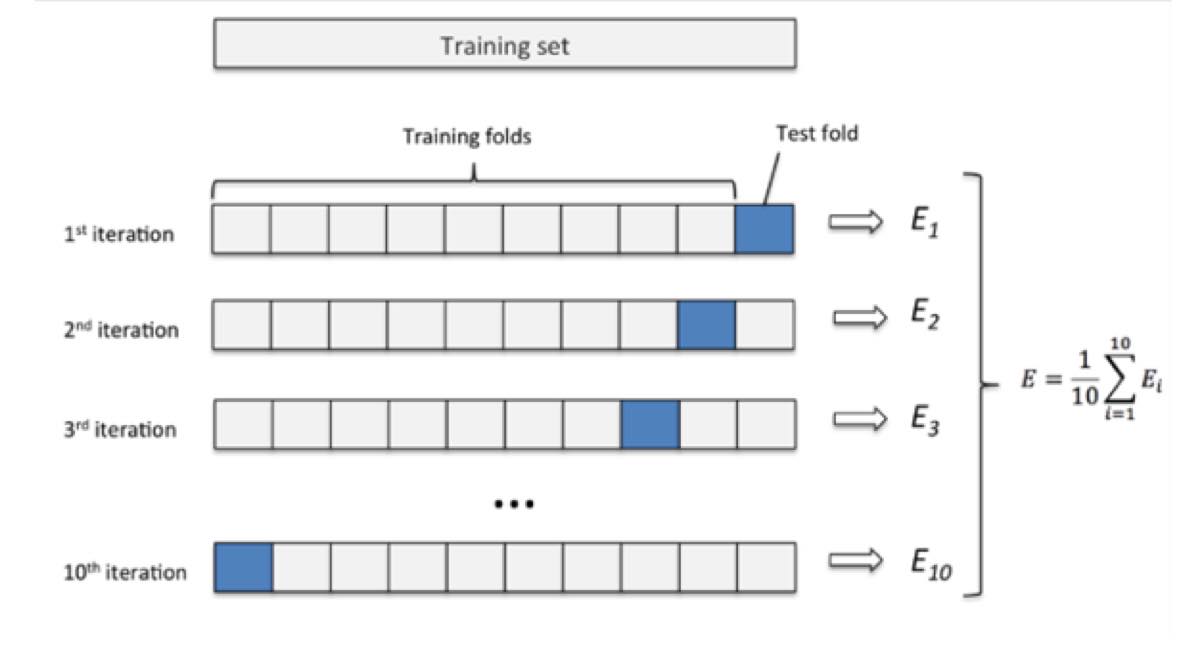

十一、过拟合与正则化

过拟合

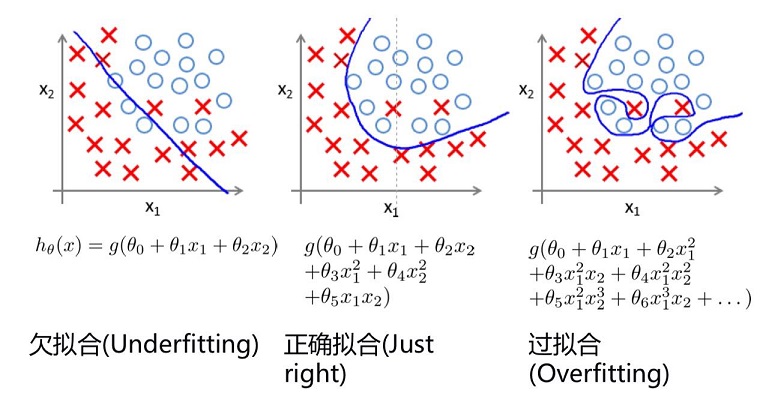
防止过拟合：

1. 减少特征

2. 增加数据量

3. 正则化

4. 深度学习中有其他防止过拟合的方式

正则化

L1 正则化：$\displaystyle J (\theta)={1 \over m} \sum_{i=0}^m (h_\theta (x_i)-y_i)^2 + \lambda\sum_{i=0}^n |\theta_j|$

L2 正则化：$\displaystyle J (\theta)={1 \over m} \sum_{i=0}^m (h_\theta (x_i)-y_i)^2 + \lambda\sum_{i=0}^n \theta_j^2$

十二、岭回归

概念

在使用标准方程解多元线性回归的时候，$w=(X^TX)^{-1} X^Ty$
如果数据的特征比样本点还多，数据特征 $n$ 个，样本个数 $m$ 个，如果 $n>m$
，则计算 $(X^TX)^{-1}$ 时会出错。因为 $(X^TX)$ 不是满秩矩阵，所以不可逆。
为了解决这个问题，统计学家引入了岭回归的概念。
$w=(X^TX+\lambda I)^{-1} X^Ty$
$\lambda$ 为岭系数，$I$ 为单位矩阵

推导

岭回归的代价函数是 L2 正则化：$\displaystyle J (\theta)={1 \over m} \sum_{i=0}^m (h_\theta (x_i)-y_i)^2 + \lambda\sum_{i=0}^n \theta_j^2$
$\displaystyle J (\theta)={1 \over 2} (w^TX^TXw - y^TXw - w^TX^Ty + y^Ty) + \lambda \theta^T\theta$

$\displaystyle {\partial J (\theta) \over \partial \theta}=0$

$X^TX\theta - X^TY + \lambda \theta=0$
$\theta=(X^TX+\lambda I)^{-1} X^TY$

用处

岭回归最早是用来处理特征数多于样本的情况，现在也用于在估计中加入偏差，从而得到更好的估计。
同时也可以解决多重共线性的问题。
岭回归是一种有偏估计。

$\lambda$ 的选择

选择 $\lambda$ 值，使得
(1) 各个回归系数的岭估计基本稳定
(2) 残差平方和增大不太多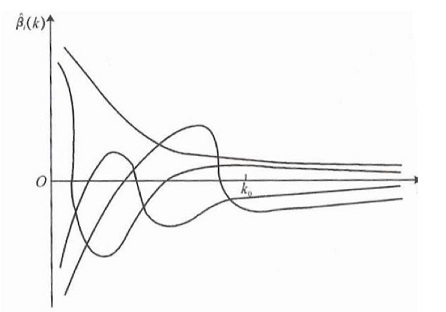

横轴是 $\lambda$ 值，纵轴是参数 $\theta$ 的取值范围

\# 创建模型
\# 生成 50 个值（默认是 50 个值）
alphas_to_test = np.linspace (0.001, 1)
\# 创建模型，保存误差值
model = linear_model.RidgeCV (alphas=alphas_to_test, store_cv_values=True)
//CV 是交叉验证法的意思，可是设置 alphas
model.fit (x_data, y_data)

\# 岭系数
print (model.alpha_)
\# loss 值
print (model.cv_values_.shape)

\# 画图
\# 岭系数跟 loss 值的关系
plt.plot (alphas_to_test, model.cv_values_.mean (axis=0))
\# 选取的岭系数值的位置
plt.plot (model.alpha_, min (model.cv_values_.mean (axis=0)),'ro')
plt.show ()

十三、LASSO 算法

概念

通过构造一个一阶惩罚函数获得一个精炼的模型；通过最终确定一些指标（变量）的系数为零（岭回归估计系数等于 0 的机会微乎其微，造成筛选变量困难），解释力很强。
擅长处理具有多重共线性的数据，与岭回归一样是有偏估计。

LASSO 的代价函数

$\displaystyle J (\theta)={1 \over m} \sum_{i=0}^m (h_\theta (x_i)-y_i)^2 + \lambda\sum_{i=0}^n |\theta_j|$
$\lambda$ 的值可以用于限制 $\sum_{i=0}^n |\theta_j| \leq t$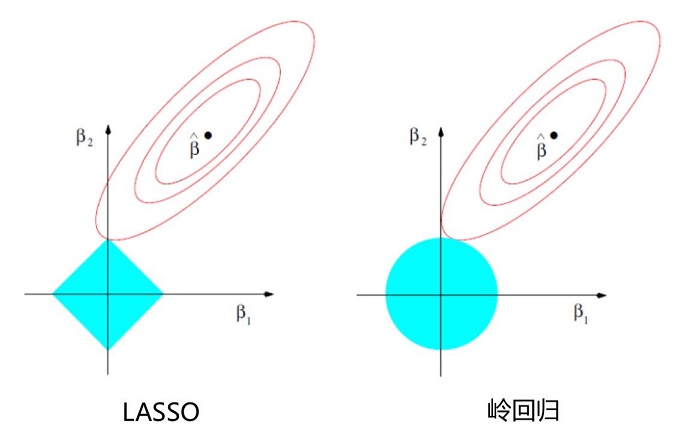

一圈圈椭圆是 loss 函数的等高线，最中间的 $\beta$ 值使得 loss 函数最小
由图中可以观察出，lasso 算法容易使得某些 $\beta$ 取值为零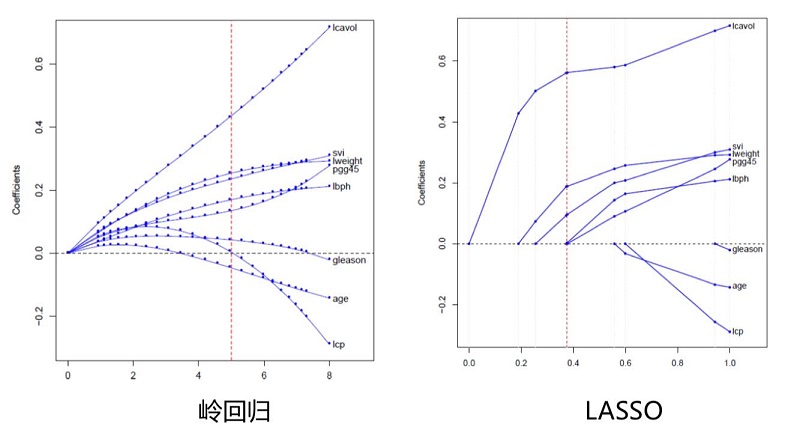

十四、弹性网

代价函数

$\displaystyle J (\theta)={1 \over m} \sum_{i=0}^m (h_\theta (x_i)-y_i)^2 + \lambda\sum_{i=0}^n |\theta_j|^q$

机器学习算法系列

机器学习算法 —（1）线性回归和非线性回归
 机器学习算法 —（2）逻辑回归
 机器学习算法 —（3）神经网络
 机器学习算法 —（4）KNN
机器学习算法 —（5）决策树
 机器学习算法 —（6）集成学习
 机器学习算法 —（7）贝叶斯算法
 机器学习算法 —（8）聚类算法
 机器学习算法 —（9）主成分分析 PCA
机器学习算法 —（10）支持向量机 SVM

梯度下降法	标准方程法
缺点：需要选择合适的学习率需要迭代很多个周期只能得到最优解的近似值	优点：不需要学习率不需要迭代可以得到全局最优解
优点：当特征值非常多的时候也可以很好的工作	缺点：需要计算 $(𝑋^T𝑋)^{−1}$ 时间复杂度大约是 O ($n^3$) n 是特征数量

前言