机器学习算法 --（2）逻辑回归

發表於 更新於 分類於

一、预测函数

预测函数 $h_\theta (x)=g (\theta^Tx)$
$\displaystyle g (x)={1 \over {1+e^{-x}}}$ $\quad \quad$ $\displaystyle h_\theta (x)={1 \over {1+e^{-\theta^Tx}}}$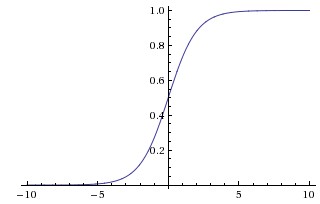

二、代价函数

线性回归：$\displaystyle J (\theta)={1 \over m}\sum_{i=0}^m {1 \over 2}(h_\theta (x_i)-y_i)^2$
逻辑回归：$cost (h_\theta (x), y)=
\begin {cases}
-log (h_\theta (x)), & \text {if $y=1$} \\
-log (1-h_\theta (x)), & \text {if $y=0$}
\end {cases}$

$cost (h_\theta (x), y)=-y \, log (h_\theta (x))-(1-y) log (1-h_\theta (x))$
$\displaystyle J (\theta)=-{1 \over m}[\sum_{i=0}^m \, log (h_\theta (x))-(1-y) log (1-h_\theta (x))]$

梯度下降法

$Repeat$
$\lbrace$
$\quad \theta_j := \theta_j - \alpha {\partial \over \partial \theta_j} J (\theta)$
$\rbrace$

$cost (h_\theta (x), y)=-y \, log (h_\theta (x))-(1-y) log (1-h_\theta (x))$

$\displaystyle {\partial cost (h_\theta (x), y) \over \partial \theta}$
$\displaystyle =-{1 \over m} \sum_{i=0}^m ({y \over h_\theta (x)} - {(1-y) \over 1-h_\theta (x)}) {\partial h_\theta (x) \over \partial \theta}$
$=\displaystyle =-{1 \over m} \sum_{i=0}^m ({y \over h_\theta (x)} - {(1-y) \over 1-h_\theta (x)}) h_\theta’(x) x$
$=\displaystyle {1 \over m} \sum_{i=0}^m {h_\theta’(x) x \over h_\theta (x)(1-h_\theta (x))}(h_\theta (x) - y)$
$=\displaystyle {1 \over m} \sum_{i=0}^m x (h_\theta (x)-y)$

三、多分类

可以分别做若干次二分类

四、逻辑回归正则化

代价函数：$\displaystyle J (\theta)=-{1 \over m}[\sum_{i=0}^my \, log (h_\theta (x))-(1-y) log (1-h_\theta (x))] + {\lambda \over 2m} \sum_{i=0}^m \theta_j^2$

五、正确率 / 召回率 / F1 指标

正确率 Precision：检索出来的条目有多少是正确的
召回率 Recall：正确的条目有多少被检索出来了
$\displaystyle F_1 值 ={2 \times {正确率 + 召回率 \over 正确率 \times 召回率}}$
正确率和召回率有时候是矛盾的，所以在不同场合需要自己判断正确率或是召回率的重要性
$\displaystyle F_\beta={(1+\beta^2) \times {正确率 + 召回率 \over (\beta^2 \times 正确率) \times 召回率}}$

六、sklearn 实战逻辑回归

1
2
3
4
5
6
7
8
9
10
11
12
13
logistic = linear_model.LogisticRegression ()
logistic.fit (x_data, y_data)

if scale == False:
    # 画图决策边界
    plot ()
    x_test = np.array ([[-4],[3]])
    y_test = (-logistic.intercept_ - x_test*logistic.coef_[0][0])/logistic.coef_[0][1]
    plt.plot (x_test, y_test, 'k')
    plt.show ()

predictions = logistic.predict (x_data)
print (classification_report (y_data, predictions))

七、sklearn 实战非线性逻辑回归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
logistic = linear_model.LogisticRegression ()
logistic.fit (x_data, y_data)

# 获取数据值所在的范围
x_min, x_max = x_data [:, 0].min () - 1, x_data [:, 0].max () + 1
y_min, y_max = x_data [:, 1].min () - 1, x_data [:, 1].max () + 1
# 生成网格矩阵
xx, yy = np.meshgrid (np.arange (x_min, x_max, 0.02),
                     np.arange (y_min, y_max, 0.02))
# ravel 与 flatten 类似，多维数据转一维。flatten 不会改变原始数据，ravel 会改变原始数据
z = logistic.predict (np.c_[xx.ravel (), yy.ravel ()])
z = z.reshape (xx.shape)
# 等高线图
cs = plt.contourf (xx, yy, z)
# 样本散点图
plt.scatter (x_data [:, 0], x_data [:, 1], c=y_data)
plt.show ()
print ('score:',logistic.score (x_data,y_data))

机器学习算法系列

机器学习算法 —（1）线性回归和非线性回归
机器学习算法 —（2）逻辑回归
机器学习算法 —（3）神经网络
机器学习算法 —（4）KNN
机器学习算法 —（5）决策树
机器学习算法 —（6）集成学习
机器学习算法 —（7）贝叶斯算法
机器学习算法 —（8）聚类算法
机器学习算法 —（9）主成分分析 PCA
机器学习算法 —（10）支持向量机 SVM