机器学习算法 --（3）神经网络

發表於 更新於 分類於

一、深度学习

1. 深度学习三次热潮

1950 年代：图灵提出图灵测试
1980 年代：李开复语音识别，BP 算法
2006 年至今：李飞飞 ImageNet，AlphoGo 战胜人类棋手

2. 深度学习爆发三要素

数据、算法、算力

3. 机器学习三巨头

Hinton：BP 算法
Lecun：卷积神经网络
Bengio：预训练和自动编码器
吴恩达：创建 Coursera 和 Google Brain

二、单层感知机

1. 介绍


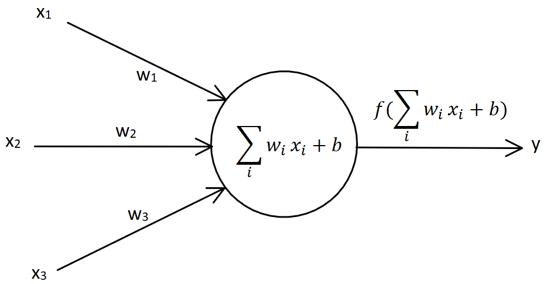
$\Delta w_i = \eta (t-y) x_i$
输入节点：$x_1, x_2, x_3$
输出节点：$y$
权向量：$w_1, w_2, w_3$
偏置因子：$b$（也可以看成是 $x_0=1$）
激活函数：$sign (x) =
\begin {cases}
1, & \text {$x \geq 0$} \\
-1, & \text {x < 0}
\end {cases}
$

2. 例子：sklearn 实现单层感知器

题目：假设平面坐标系上有四个点，$(3,3),(4,3)$ 这两个点的标签为 $1$；$(1,1),(0,2)$ 这两个点的标签为 $-1$。构建神经网络来分类。

思路：我们要分类的数据是 $2$ 维数据，所以只需要 $2$ 个输入节点，我们可以把神经元的偏置值也设置成一个节点，这样我们需要 $3$ 个输入节点。输入数据有 $4$ 个 $(1,3,3),(1,4,3),(1,1,1),(1,0,2)$ 数据对应的标签为 $(1,1,-1,-1)$。初始化权值 $w_0,w_1,w_2$，取 $-1$ 到 $1$ 的随机数。学习率设置为 $0.11$，激活函数为 sign 函数。

程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# n 个输入，m 个输出，权值矩阵就设置成 nXm 大小 
# 权值初始化，3 行 1 列，取值范围 - 1 到 1
W = (np.random.random ([3,1])-0.5)*2

print (W)
# 学习率设置
lr = 0.11
# 神经网络输出
O = 0

def update ():
    global X,Y,W,lr
    O = np.dot (X,W) # shape:(3,1)
    W_C = lr*(X.T.dot (Y-O))/int (X.shape [0])
    W = W + W_C

for i in range (100):
    update ()# 更新权值

# 计算分界线的斜率以及截距
k = -W [1]/W [2]
d = -W [0]/W [2]
plt.figure ()
plt.plot (xdata,xdata*k+d,'r')
plt.scatter (x1,y1,c='b')
plt.scatter (x2,y2,c='y')
plt.show ()

问题：单层感知器没办法解决异或问题
有三种情形，跳出循环：
(1) 实际输出等于期望输出
(2) 权值的该变量比较小的时候
(3) 循环一定次数之后

三、线性神经网络

1. 概念

线性神经网络在结构上和感知器非常类似，只是激活函数不同。
在模型训练时把原来激活函数 sign 函数改成 purelin 函数：$y=x$

2. 代价函数（损失函数）

二次代价函数：$\displaystyle E={1 \over 2} (t-y)^2={1 \over 2} [t-f (WX)]^2$
误差 E 是权值向量 $W$ 的函数，我们可以使用梯度下降法来最小化 $E$ 的值：
$\Delta W = -\eta E’ = \eta X^T (t-y) f’(WX) = \eta X^T \delta$
$\Delta w_i = -\eta E’ = \eta x_i X^T (t-y) f’(WX) = \eta \, x_i \delta$

3.sklearn 实现线性神经网络

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# n 个输入，m 个输出，权值矩阵就设置成 nXm 大小
# 权值初始化，3 行 1 列，取值范围 - 1 到 1
W = (np.random.random ([3,1])-0.5)*2

print (W)
# 学习率设置
lr = 0.11
# 神经网络输出
O = 0

def update ():
    global X,Y,W,lr
    O = np.sign (np.dot (X,W)) # shape:(3,1)
    W_C = lr*(X.T.dot (Y-O))/int (X.shape [0])
    W = W + W_C

for i in range (100):
    update ()# 更新权值
    O = np.sign (np.dot (X,W))# 计算当前输出  
    if (O == Y).all (): # 如果实际输出等于期望输出，模型收敛，循环结束
        print ('Finished')
        print ('epoch:',i)
        break

# 计算分界线的斜率以及截距
k = -W [1]/W [2]
d = -W [0]/W [2]
plt.figure ()
plt.plot (xdata,xdata*k+d,'r')
plt.scatter (x1,y1,c='b')
plt.scatter (x2,y2,c='y')
plt.show ()

四、BP 神经网络

网络结构


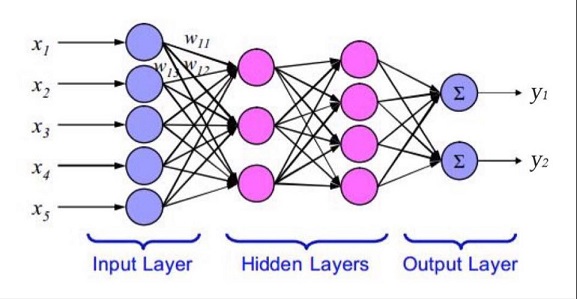
通常有三层，输入不算一层

BP 算法

$Delta$ 学习规则：$\displaystyle E={1 \over 2} (t-y)^2$
$\displaystyle {\partial E \over \partial W^l} = -(X^l)^T \delta^l \quad \quad \Delta W^l = -\eta {\partial E \over \partial W^l} = \eta (X^l)^T \delta^l$

Q：为什么 ReLU 是常用的激活函数？
因为其他的激活函数会导致导数趋近于 0，反向传播的时候权值的改变就会趋近于 0
如果神经网络的层数过多，也容易导致传播到前面的层数的时候，权值的该变量趋近于 0
Q：线性激活函数 $y=x$ 的导数也是等于 1，为什么不用？因为不能描述复杂的边界

BP 算法推导

机器学习算法系列

机器学习算法 —（1）线性回归和非线性回归
机器学习算法 —（2）逻辑回归
机器学习算法 —（3）神经网络
机器学习算法 —（4）KNN
机器学习算法 —（5）决策树
机器学习算法 —（6）集成学习
机器学习算法 —（7）贝叶斯算法
机器学习算法 —（8）聚类算法
机器学习算法 —（9）主成分分析 PCA
机器学习算法 —（10）支持向量机 SVM