slam 基础 --(4)特征检测和追踪
一、Reference Frame 参考坐标
1.Inertial Frame
(1) Earth-Centered Inertial frame (ECI)
(2) Earth-Centered and Earth-Fixed Inertial Frame
X 轴固定在地球表面随着地球转动而转动
最常见的地球坐标系
2.Earth-Fixed Frame 局部地理坐标系 / 世界坐标系
原点在地球表面
3.Body-fixed Frame (Body Frame)
坐标原点在机体上
坐标原点是自己定义的 ex: 在图像传感器中心
最后算出来的姿态和定义的坐标系有关
二、Rigid Transformation
刚体变换 = 旋转变换 + 平移变换 $x’=Rx+t$
刚体变换保长度、保角度
证明旋转矩阵都是正交矩阵,反之则否
旋转矩阵 (Rotate Matrix) 的性质分析
正交矩阵都是旋转矩阵吗?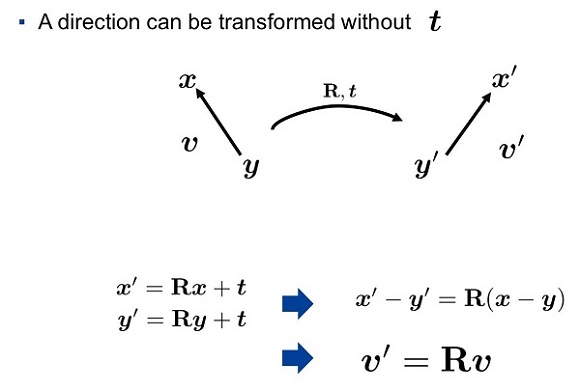
1.Pose representation 位姿
位姿可以用刚体变换描述
2.Body-to-world transformation (机器人用的比较多)
$
x_w=
\begin {bmatrix}
R_1 & R_2 & R_3 \\
R_4 & R_5 & R_6 \\
R_7 & R_8 & R_9 \\
\end {bmatrix}
x+t
$
旋转矩阵的第一 column 表示 body 坐标系 X 轴在世界坐标系下投影
(Column vectors in $R$ are the directions of body axes in the world frame)
$t$ 代表体坐标系原点投影在世界坐标系的坐标
3.World-to-body transformation (计算机视觉用的比较多)
$
x=
\begin {bmatrix}
R_1 & R_2 & R_3 \\
R_4 & R_5 & R_6 \\
R_7 & R_8 & R_9 \\
\end {bmatrix}
x_w+t
$
旋转矩阵的第一 row 表示 body 坐标系 X 轴在世界坐标系下投影
(Row vectors in $R$ are the directions of body axes in the world frame)
$x_w^0=-R^T t$
三、Projective geometry
1.Homogenous coordinates
描述比较简洁 ex: 一个矩阵就可以描述刚体变换
可以描述笛卡尔坐标系无法描述的元素 ex: 无穷远的点
齐次坐标在《图形学》应用广泛
$
\left [\begin {matrix}
x’ \\
1 \\
\end {matrix}\right] \sim
\left [\begin {matrix}
R & t \\
0^T & 1 \\
\end {matrix}\right]
\left [\begin {matrix}
x \\
1 \\
\end {matrix}\right]
$
2.2D projective geometry 之坐标表示
在二维空间中点和线是对偶关系
点的表达:$\mathbf {x}=(x,y,1)^T$
线的表达 $ax+by+c$:$\mathbf {l}=(a,b,c)^T$
两线交点:两条线叉乘
两个点连成一条线:兩个点叉乘
无穷远点:两个平行线交点
无穷远线
3.2D projective geometry 之 homography matrix (实现点的变换)
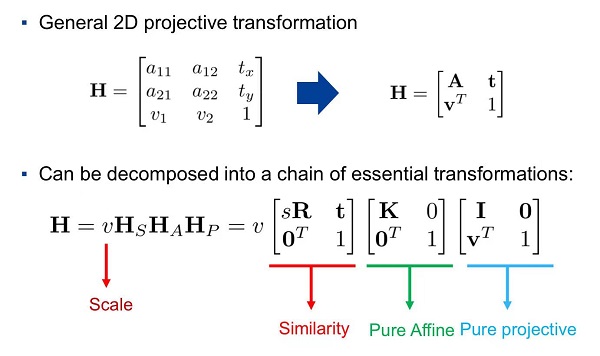
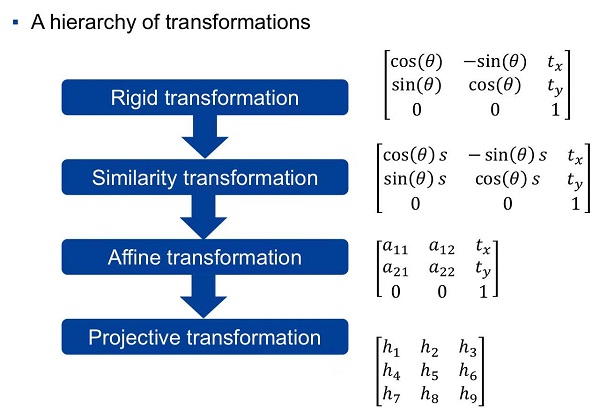
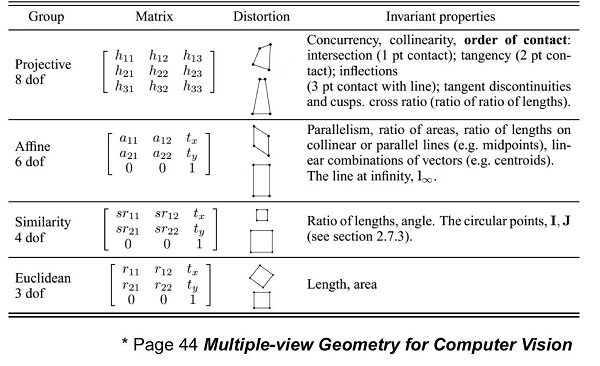
(1) 刚体变换:保长度,保角度
刚性变换:只由平移变换和旋转变换组成。
(2) 相似变换:保比例
(3) 仿射变换主要包括平移变换、旋转变换、缩放变换、错切变换、翻转变换,有六个自由度。
仿射变换保持二维图形的 “平直性” 和 “平行性”,但是角度会改变。
“平直性”:变换后直线还是直线、圆弧还是圆弧。
“平行性”:平行线还是平行线,直线上点的位置顺序不变。
(4) 射影变换 (投影变换)
射影变换:是最一般的线性变换。有 8 个自由度。
射影变换保持重合关系和交比不变。但不会保持平行性。
交比不变 (顺便学习射影几何)
[射影幾何] 交比 (Cross Ratio)
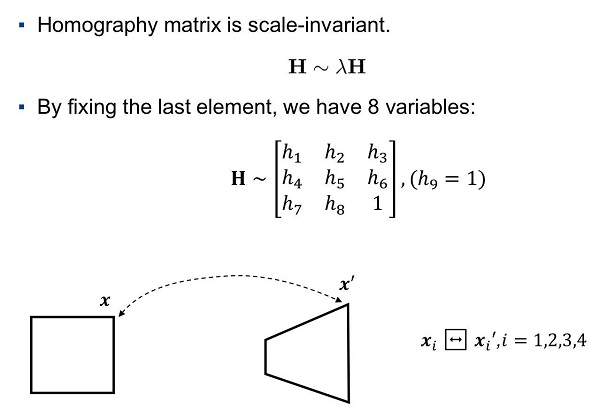

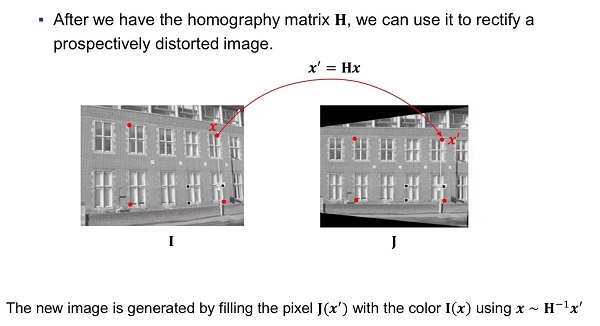
step1: 找出两幅图像之间的单应矩阵
step2: 逐行扫描图像二中的像素,透过单应矩阵找出与之对应在图像一中的像素
利用该像素的值对图像一的像素进行着色,如果对应过去是亚像素则进行插值
Q: 线条的变换?
4.3D projective geometry
在三维空间中点和面是对偶关系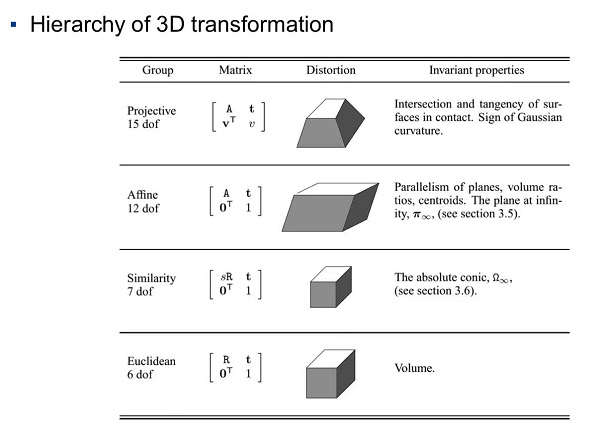
(1) 三维点的表示:
(2) 三维平面的表示:
(3) 三个点形成一平面:
(4) 三个平面确定一个交点:
(5) 三维平面的变换:
[补充 动三维空间刚体运] 一、旋转矩阵
1. 点、向量、坐标系
大部分 3D 程序库使用右手系 (如 OpenGL、3DMax 等),
也有部分库使用左手系 (如 Unity、Direct3D 等)
$a \dot b$
$
a \times b =
\begin {Vmatrix}
\mathbf {e_1} & \mathbf {e_2} & \mathbf {e_3} \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3 \\
\end {Vmatrix} =
\left [\begin {matrix}
a_2 b_3 - a_3 b_2 \\
a_3 b_1 - a_1 b_3 \\
a_1 b_2 - a_2 b_1 \\
\end {matrix}\right] =
\left [\begin {matrix}
0 & -a_3 & a_2 \\
a_3 & 0 & -a_1 \\
-a_2 & a_1 & 0 \\
\end {matrix}\right] \mathbf {b} \overset {def}{=}
a
$^$b$
latex 等号上面有字 \overset {def}{=}