Nathan's whisper

问题：例如梯度下降法更新参数，如果参数是旋转量，怎么更新这个参数？

一、Parameter update

1.

2.

3.

二、Rotation matrix

1. 旋转矩阵是属于 $SO (n)$ 群

Special Orthogonal group SO (n) is a set that satisfies:
$SO (n)=\{\mathbf {M} \in \mathbb {R} | \mathbf {M}\mathbf {M}^T=\mathbf {I},det (\mathbf {M})=1\}$
A 3x3 rotation matrix is in the SO (3) group
MathJax 支持的 Latex 符号总结（各种数学字体）

2. 什么是群

A group $G$ is a set with a binary operation $\circ$ defined on the elements of $G$, if it satisfies:
Closure: $g_1 \circ g_2 \in G$
Identity: $e \circ g = g \circ e = e$
Inverse: $g \circ g^{-1} = g^{-1} \circ g = e$
Associativity: $g_1 \circ (g_2 \circ g_3) = (g_1 \circ g_2) \circ g_3$
LaTeX 各种命令，符号
Latex 使用说明 数学公式

三、Lie group SO (3) / Lie algebra so (3)

1.

2.

3.

四、Euler angles

1.

2.

3.

五、Quaternion

1.

2.

3.

一、Reference Frame 参考坐标

1.Inertial Frame

(1) Earth-Centered Inertial frame (ECI)
(2) Earth-Centered and Earth-Fixed Inertial Frame
X 轴固定在地球表面随着地球转动而转动
最常见的地球坐标系

2.Earth-Fixed Frame 局部地理坐标系 / 世界坐标系

原点在地球表面

3.Body-fixed Frame (Body Frame)

坐标原点在机体上
坐标原点是自己定义的 ex: 在图像传感器中心
最后算出来的姿态和定义的坐标系有关

二、Rigid Transformation

刚体变换 = 旋转变换 + 平移变换 $x’=Rx+t$
刚体变换保长度、保角度
证明旋转矩阵都是正交矩阵，反之则否
旋转矩阵 (Rotate Matrix) 的性质分析
正交矩阵都是旋转矩阵吗？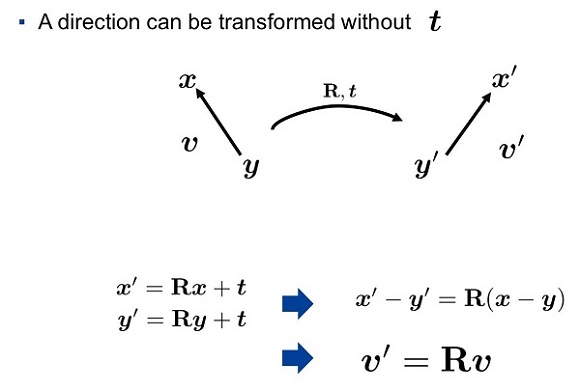

1.Pose representation 位姿

位姿可以用刚体变换描述

2.Body-to-world transformation (机器人用的比较多)

$
x_w=
\begin {bmatrix}
R_1 & R_2 & R_3 \\
R_4 & R_5 & R_6 \\
R_7 & R_8 & R_9 \\
\end {bmatrix}
x+t
$
旋转矩阵的第一 column 表示 body 坐标系 X 轴在世界坐标系下投影
(Column vectors in $R$ are the directions of body axes in the world frame)
$t$ 代表体坐标系原点投影在世界坐标系的坐标

3.World-to-body transformation (计算机视觉用的比较多)

$
x=
\begin {bmatrix}
R_1 & R_2 & R_3 \\
R_4 & R_5 & R_6 \\
R_7 & R_8 & R_9 \\
\end {bmatrix}
x_w+t
$
旋转矩阵的第一 row 表示 body 坐标系 X 轴在世界坐标系下投影
(Row vectors in $R$ are the directions of body axes in the world frame)
$x_w^0=-R^T t$

三、Projective geometry

1.Homogenous coordinates

描述比较简洁 ex: 一个矩阵就可以描述刚体变换
可以描述笛卡尔坐标系无法描述的元素 ex: 无穷远的点
齐次坐标在《图形学》应用广泛

$
\left [\begin {matrix}
x’ \\
1 \\
\end {matrix}\right] \sim
\left [\begin {matrix}
R & t \\
0^T & 1 \\
\end {matrix}\right]
\left [\begin {matrix}
x \\
1 \\
\end {matrix}\right]
$

2.2D projective geometry 之坐标表示

在二维空间中点和线是对偶关系
点的表达：$\mathbf {x}=(x,y,1)^T$
线的表达 $ax+by+c$：$\mathbf {l}=(a,b,c)^T$
两线交点：两条线叉乘
两个点连成一条线：兩个点叉乘
无穷远点：两个平行线交点
无穷远线

3.2D projective geometry 之 homography matrix (实现点的变换)

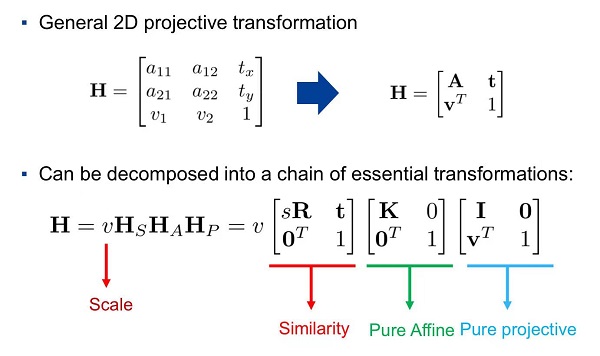
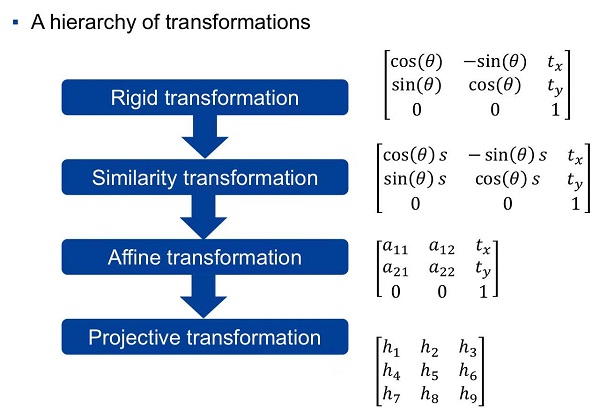
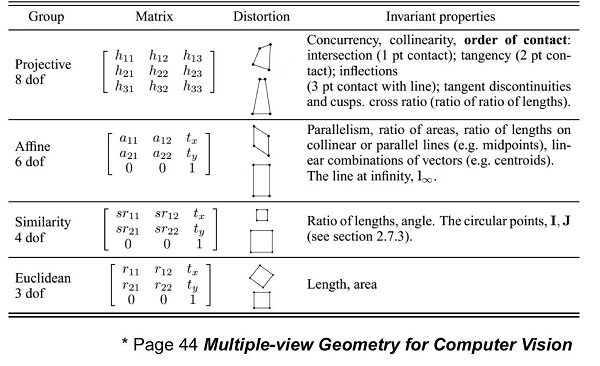
(1) 刚体变换：保长度，保角度
刚性变换：只由平移变换和旋转变换组成。
(2) 相似变换：保比例
(3) 仿射变换主要包括平移变换、旋转变换、缩放变换、错切变换、翻转变换，有六个自由度。
仿射变换保持二维图形的 “平直性” 和 “平行性”，但是角度会改变。
“平直性”：变换后直线还是直线、圆弧还是圆弧。
“平行性”：平行线还是平行线，直线上点的位置顺序不变。
(4) 射影变换 (投影变换)
射影变换：是最一般的线性变换。有 8 个自由度。
射影变换保持重合关系和交比不变。但不会保持平行性。
交比不变 (顺便学习射影几何)
[射影幾何] 交比 (Cross Ratio)

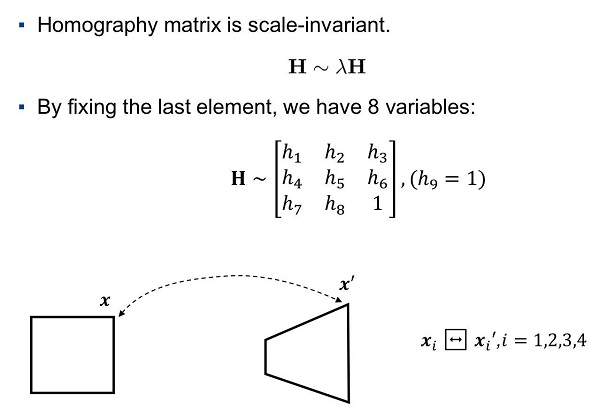
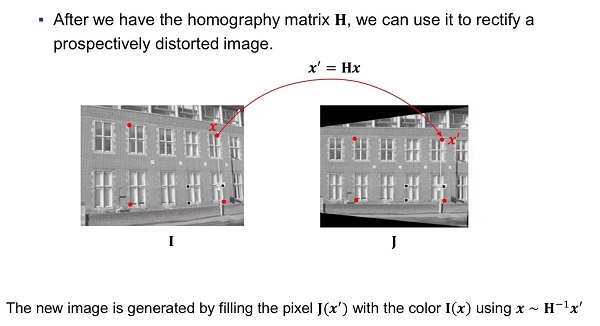
step1: 找出两幅图像之间的单应矩阵
step2: 逐行扫描图像二中的像素，透过单应矩阵找出与之对应在图像一中的像素
利用该像素的值对图像一的像素进行着色，如果对应过去是亚像素则进行插值
Q: 线条的变换？

4.3D projective geometry

在三维空间中点和面是对偶关系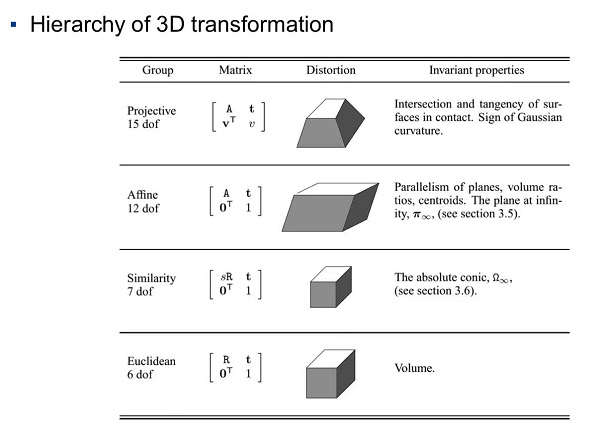

(1) 三维点的表示：
(2) 三维平面的表示：
(3) 三个点形成一平面：
(4) 三个平面确定一个交点：
(5) 三维平面的变换：

[补充 动三维空间刚体运] 一、旋转矩阵

1. 点、向量、坐标系

大部分 3D 程序库使用右手系 (如 OpenGL、3DMax 等)，
也有部分库使用左手系 (如 Unity、Direct3D 等)
$a \dot b$
$
a \times b =
\begin {Vmatrix}
\mathbf {e_1} & \mathbf {e_2} & \mathbf {e_3} \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3 \\
\end {Vmatrix} =
\left [\begin {matrix}
a_2 b_3 - a_3 b_2 \\
a_3 b_1 - a_1 b_3 \\
a_1 b_2 - a_2 b_1 \\
\end {matrix}\right] =
\left [\begin {matrix}
0 & -a_3 & a_2 \\
a_3 & 0 & -a_1 \\
-a_2 & a_1 & 0 \\
\end {matrix}\right] \mathbf {b} \overset {def}{=}
a
$^$b$

latex 等号上面有字 \overset {def}{=}

2. 坐标矩阵间的欧式变换

3.

增强处理的方法：大致可分为三大类

1. 点变换：只与本身像素点的值有关，做灰度值变换，与空间邻点值无关。
2. 空间域处理：往往作邻域加权和处理
   ・需考虑邻域大小、形状
   ・点变换可看作处理窗为 1×1 的空间域处理
3. 频域处理

一、灰度变换

1. 直方图

最常用的像素统计特性描述方式

2. 灰度增强

灰度增强就是按照一定变换方式逐点地改变原来图像中每个像素的灰度值 $r’=T (t)$。
通过改变像素灰度值获得直方图形状的改变。
(1) 灰度线性变换
(2) 灰度非线性变换
离散图像

一、视觉系统

1. 色彩是一种光的视觉效应

这句话蕴含了两层含义，首先，色彩依赖于场景发射或者反射的可见光，但这还不够，还需要经过人的视觉系统处理过后，才能得到可见光对应的视觉效应。注意，这种对应并不是一一映射。

2. 视杆 (rod) 细胞和视锥 (cone) 细胞

在眼睛中用于感受光的细胞有两种，视杆（rod）细胞和视锥（cone）细胞，其中视杆细胞不区分光线波长，主要在低光时起作用（猫咪的视杆细胞就超级多，所以它们暗光视觉很棒），分布在视网膜中心凹的边缘。而视锥细胞则对波长敏感，按照敏感波长为三种：长、中、短，分布在视网膜的中间。

无穷维的 SPD 在三维上 (三种不同的视锥细胞) 的投影，就是我们所能感受到的色彩空间，这也解释了为什么我们在表示色彩时总是会取三个参数。

3. 格拉斯曼定律 (Grassmann’s law)

人眼看到的色彩具有很强的线性加和性质。

4. 闪烁混合测试 (Flicker Fusion Test)

其目的是得到人对不同波长光的感受亮度，得到不同波长下的敏感度分布曲线。
这条曲线又被称为光度函数 (luminosity function)，记作 y-bar ($\lambda$) 或者 V ($\lambda$)

5. 色彩匹配实验 (Metameric Matches)

目的是量化所有的可见颜色。
测试单色光 vs 可调整的光。
可调整的光是三种单色光的混合，他们波长固定（700 nm, 546 nm, 435 nm）强度可调节，并称这三个波长为原色。 选择 546.1 nm 和 435.8 nm 的原色是因为它们是汞蒸气放电的颜色，容易复现，而选择 700 nm 是因为眼睛在 700 nm 处对光线的变化不敏感，波长的误差对感知的影响不大。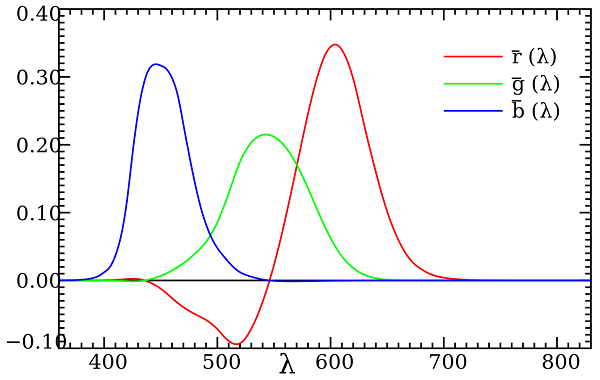


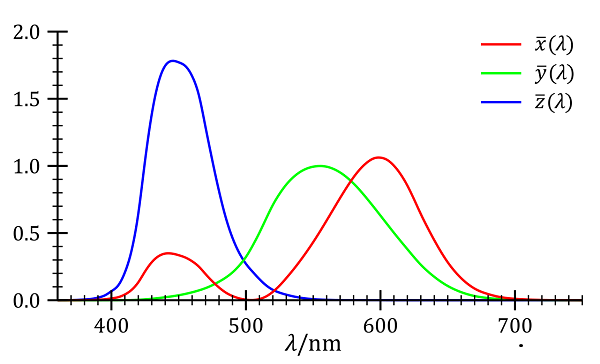
相机图像处理 1 色彩与色彩空间

6.HSI 顏色模型 HSI〔Hue-Saturation-Intensity (Lightness),HSI 或 HSL〕

7.YUV 坐标系

$Y$: 亮度
$C_b,C_r$：色差
(R-Y),(B-Y),(G-Y) 可从中选取两个。但由于对大多数彩色来说，(G-Y) 比 (R-Y),(B-Y) 数值还小，选择 (G-Y) 对改善信号比不利。通常选用 (R-Y) 和 (B-Y) 两个色差信号来代表色度信息。

二、图像质量评估

1. 图像质量

(1) 平均亮度
(2) 对比度
一幅图像中灰度反差的大小。对比度 = 最大亮度 / 最小亮度。
(3) 清晰度
应用：用传统方法做超分辨率图像
(4) 分辨度

2. 客观评价指标

PSNR (Peak Signal to Noise Ratio)：峰值信噪比
$\displaystyle PSNR=10log_{10} \frac {MaxValue^2}{MSE}$

$\displaystyle =10log_{10} \frac {(2^{bits}-1)^2}{\frac {1}{MN} \sum_{i=0}^{M-1} \sum_{i=0}^{N-1}{[f (m,n)-g (m,n)]}}$

MSE (Mean squared error)：均方误差
SSIM (Structural Similarity)：强调结构相似性
图像质量评估指标 SSIM / PSNR / MSE
视频 / 图像质量评价综述 (一)

3. 主观评价指标

MOS (mean opinion score)

一、

1.

2.

3.

二、

三、

四、

五、

代数变换应用：

1. 提取前景物体（帧差法、背景差分法、GMM、Vibe、稀疏表示）
   几何变换应用：
2. 图像拼接（立体图特征点匹配、要有 overlap、SIFT 不受尺度和旋转的变化、特征点可以看成一个向量、求解单应矩阵）
3. 虚拟视生成
4. 图像变形

一、成像原理

1.

2.

3.

二、采样与量化

三、人眼视觉特性

1. 光度学基本原理

人眼对 380～780 纳米内不同波长的光具有不同的敏感程度，称为人眼的视敏特性。 衡量描述人眼视敏特性的物理量为视敏函数和相对视敏函数。
(1) 视敏函数 在相同亮度感觉的条件下，不同波长上光辐射功率的倒数可以用来衡量人眼对各波长光明亮感觉的敏感程度，称为视敏函数。
$K (\lambda)={1 \over p_r (\lambda)}$
(2) 相对视敏函数 实验表明，人眼对波长为 555 纳米的光最敏感，因此把任意波长的光的视敏函数与最大视敏函数值 K (555) 相比的比值称为相对视敏函数。
$V (\lambda)={K (\lambda) \over k_max}={K (\lambda) \over K (555)}={P_r (555) \over P_r (\lambda)}$
人眼视觉特性

2. 人眼视觉特性

3. 人眼视觉模型

4. 彩色图像的表示

四、

五、

一、

1.

2.

3.

二、

三、

四、

五、

一、特征点

1. 好的特征点：稳定、可识别、精确

2. 特征检测和描述

3. 特征匹配和追踪

二、光流算法

三、FAST (Corner detector)

四、LoG/DoG/MSER (Blob detector)

五、BRIEF/ORB/BRISK/FREAK (fast descriptor)

六、SIFT/SURF/HOG (slow descriptor)

七、Learning-based features

八、Other features

九、